cancel2 2022
Canceled
Srinivasa Ramanujan was a largely self-taught pure mathematician. Hindered by poverty and ill-health, his highly original work has considerably enriched number theory. More recently his discoveries have been applied to physics, where his theta function lies at the heart of string theory.
Beginnings
Srinivasa Ramanujan was born on December 22, 1887 in the town of Erode, in Tamil Nadu, in the south east of India. His father was K. Srinivasa Iyengar, an accounting clerk for a clothing merchant. His mother was Komalatammal, who earned a small amount of money each month as a singer at the local temple. His family were Brahmins, the Hindu caste of priests and scholars. His mother ensured the boy was in tune with Brahmin traditions and culture. Although his family were high caste, they were very poor. Ramanujan’s parents moved around a lot, and he attended a variety of different elementary schools.
Early Mathematics
At age 10, Ramanujan was the top student in his district and he started high school at the Kumbakonam Town High School. Looking at the mathematics books in his school’s library, he quickly found his vocation. By age 12, he had begun serious self-study of mathematics, working through cubic equations and arithmetic and geometric series. He invented his own method of solving quartic equations.
As Ramanujan’s mathematical knowledge developed, his main source of inspiration and expertise became Synopsis of elementary results in pure mathematics by George S. Carr. This book presented a very large number of mathematical results – over 4000 theorems – but generally showed little working, cramming into its pages as many results as possible.
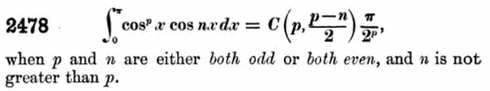
Entry 2478 from Carr’s Synopsis of elementary results in pure mathematics
With little other guidance, Ramanujan came to believe this was how mathematics was done, so he himself learned to show little working. Also, he could afford only a small amount of paper, doing most of his work on slate with chalk, transferring a minimal amount of his working and his results to paper. His memory for mathematical formulas and constants seems to have been boundless: he amazed classmates with his ability to recite the values of irrational numbers like π, e, and √2 to as many decimal places as they asked for.
An Apparently Bright Future Fizzles Out
In 1904, Ramanujan left high school; his future looked promising: he had won the school’s mathematics prize and, more importantly, a scholarship allowing him to study at the Government Arts College in the town of Kumbakonam. Obsessed with mathematics, Ramanujan failed his non-mathematical exams and lost his scholarship. In 1905, he travelled to Madras and enrolled at Pachaiyappa’s College, but again failed his non-mathematical exams.
The Discovery of Ramanujan as a Mathematician of Genius
The Hungry Years
At the beginning of 1907, at age 19, with minimal funds and a stomach all too often groaning with hunger, Ramanujan continued on the path he had chosen: total devotion to mathematics. The mathematics he was doing was highly original and very advanced.
Even though (or some might say because) he had very little formal mathematical education he was able to discover new theorems. He also independently discovered results originally discovered by some of the greatest mathematicians in history, such as Carl Friedrich Gauss and Leonhard Euler.
Ill-health was Ramanujan’s constant companion – as it would be for much of his short life.
By 1910, he realized he must find work to stay alive. In the city of Madras he found some students who needed mathematics tutoring and he also walked around the city offering to do accounting work for businesses.
And then a piece of luck came his way. Ramanujan tried to find work at the government revenue department, and there he met an official whose name was Ramaswamy Aiyer. Ramanujan did not have a resume to show Ramaswamy Aiyer; all he had were his notebooks – the results of his mathematical work.
Ramanujan’s good fortune was that Ramaswamy Aiyer was a mathematician. He had only recently founded the Indian Mathematical Society, and his jaw dropped when he saw Ramanujan’s work.

“I was struck by the extraordinary mathematical results contained in it. I had no mind to smother his genius by an appointment in the lowest rungs of the revenue department.”
https://www.famousscientists.org/srinivasa-ramanujan/
