You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
The green scene demeaned, right here on your screen
- Thread starter Diogenes
- Start date
BartenderElite
Verified User
This thread is still going?
Like the planet is in amazing shape or something?
Laughable.
Like the planet is in amazing shape or something?
Laughable.
This thread is still going?
Obs.
Do you like math?
Do you like making climate activists cry?
If so, this post is for you.
Kooky Klimate Kultists ululate endlessly about how "green" utility-scale solar photovoltaic (PV) and wind are supposed to be.
They define being “eco-friendly” as an energy technology that "emits less CO₂ over their total lifecycle".
"Emissions" are what the “greens” like to jack their sausage holsters about.
When it's pointed out to these dullards just how land-intensive their “green” energy technologies are, they squirm, trying to justify being vehemently opposed to nuclear fission — a near-infinite, carbon-free, energy-dense electricity source — and working to destroying the landscape with massive amounts of solar cells and wind farms — to "save the planet".
Let's run the numbers!
The standard nuclear reactor has a 1,000-megawatt (MW) rating.
This means that each plant is, on average, installed with 1,000 MW of power capacity. A 1,000-MW nuclear facility occupies, on average, just over 1 square mile (640 acres) of land.
To figure out just how many homes a single 1,000 MW plant could power, we can start by using the following equation: 𝑬 = 𝑷 × 𝒕, where,• 𝑬 = energy (megawatt hours, MWh)• 𝑷 = power (MW)• 𝒕 = time (hours, hr).
If we assume a 1,000 MW nuclear reactor operates at FULL power during an entire calendar year, it will produce ~8.76 terawatt-hours (TWh) of electricity per year.𝑬 = 1,000 MW × 24 hr (1-day) × 365 [days] (1 yr) = 8.76 million MWh / yr (8.76 TWh / yr).
However, reactors don't operate at full power 100% of the time because they come offline for refueling or to undergo maintenance. Therefore, we must take the capacity factor into consideration in our calculation.
According to the U.S. Energy Information Administration (EIA), nuclear power has the highest capacity factor of any electricity generation source in the U.S. at 0.93 in 2023.
https://eia.gov/electricity/annual/html/epa_04_08_b.html…
What this value means is that nuclear reactors in the U.S. operated at full installed power for about 93% of the calendar year in 2023.
So, to figure out how much electricity that each plant produces in a year, we must multiply the previously calculated value of 8.76 TWh by the capacity factor of 0.93. If we do that, we get,𝑬 = (8.76 TWh / year) × 0.93 ≈ 8.15 TWh / yr.
Now, to determine just how many homes this powers, we must divide 𝑬 by the average amount of electricity U.S. homeowners purchase in a year. According to the EIA, that number is ~10,500 kilowatt-hours (KWh) or 1.05 × 10⁻⁵ TWh.
https://eia.gov/energyexplained/use-of-energy/electricity-use-in-homes.php…
Thus, dividing 8.15 TWh / yr by 1.05 × 10⁻⁵ TWh / yr gives us about 776,190 homes.
Therefore, a 1,000 MW nuclear electricity generation station occupying one square mile of land, operating with a capacity factor of 0.93, can power more than 775,000 homes throughout the course of a year based on U.S. data.
Now that is pretty energy-dense, eh?
Why would any climate activist be opposed to that?
Do you like making climate activists cry?
If so, this post is for you.
Kooky Klimate Kultists ululate endlessly about how "green" utility-scale solar photovoltaic (PV) and wind are supposed to be.
They define being “eco-friendly” as an energy technology that "emits less CO₂ over their total lifecycle".
"Emissions" are what the “greens” like to jack their sausage holsters about.
When it's pointed out to these dullards just how land-intensive their “green” energy technologies are, they squirm, trying to justify being vehemently opposed to nuclear fission — a near-infinite, carbon-free, energy-dense electricity source — and working to destroying the landscape with massive amounts of solar cells and wind farms — to "save the planet".
Let's run the numbers!
The standard nuclear reactor has a 1,000-megawatt (MW) rating.
This means that each plant is, on average, installed with 1,000 MW of power capacity. A 1,000-MW nuclear facility occupies, on average, just over 1 square mile (640 acres) of land.
To figure out just how many homes a single 1,000 MW plant could power, we can start by using the following equation: 𝑬 = 𝑷 × 𝒕, where,• 𝑬 = energy (megawatt hours, MWh)• 𝑷 = power (MW)• 𝒕 = time (hours, hr).
If we assume a 1,000 MW nuclear reactor operates at FULL power during an entire calendar year, it will produce ~8.76 terawatt-hours (TWh) of electricity per year.𝑬 = 1,000 MW × 24 hr (1-day) × 365 [days] (1 yr) = 8.76 million MWh / yr (8.76 TWh / yr).
However, reactors don't operate at full power 100% of the time because they come offline for refueling or to undergo maintenance. Therefore, we must take the capacity factor into consideration in our calculation.
According to the U.S. Energy Information Administration (EIA), nuclear power has the highest capacity factor of any electricity generation source in the U.S. at 0.93 in 2023.
https://eia.gov/electricity/annual/html/epa_04_08_b.html…
What this value means is that nuclear reactors in the U.S. operated at full installed power for about 93% of the calendar year in 2023.
So, to figure out how much electricity that each plant produces in a year, we must multiply the previously calculated value of 8.76 TWh by the capacity factor of 0.93. If we do that, we get,𝑬 = (8.76 TWh / year) × 0.93 ≈ 8.15 TWh / yr.
Now, to determine just how many homes this powers, we must divide 𝑬 by the average amount of electricity U.S. homeowners purchase in a year. According to the EIA, that number is ~10,500 kilowatt-hours (KWh) or 1.05 × 10⁻⁵ TWh.
https://eia.gov/energyexplained/use-of-energy/electricity-use-in-homes.php…
Thus, dividing 8.15 TWh / yr by 1.05 × 10⁻⁵ TWh / yr gives us about 776,190 homes.
Therefore, a 1,000 MW nuclear electricity generation station occupying one square mile of land, operating with a capacity factor of 0.93, can power more than 775,000 homes throughout the course of a year based on U.S. data.
Now that is pretty energy-dense, eh?
Why would any climate activist be opposed to that?
Now, let's compare nuclear to the progressives' preferred solar shibboleth.
Run the numbers!
A utility-scale solar PV array requires at least 1 MW of installed power.
https://cleanpower.org/facts/solar-power/…
A1 MW solar PV array requires about 5-7 acres of land, according to the Solar Energy Industries Association (SEIA).
seia.org/initiatives/land-use-solar-development/…
Again, according to the SEIA, solar had a capacity factor of 0.232 last year in the U.S., — by far the poorest performance of any energy source.
What this means is that solar PV arrays only operated at full power 23.2% of the year in 2023 due to variable weather conditions and sky cover.
By using the same calculations as above, a 1,000 MW solar PV array would occupy some 5,000-7,000 acres of land (mean of ~6,000 acres), all the while powering 193,523 homes, some 582,667 fewer homes than if it were nuclear power.
Yikes, that doesn't sound very efficient.
Does, it?
Run the numbers!
A utility-scale solar PV array requires at least 1 MW of installed power.
https://cleanpower.org/facts/solar-power/…
A1 MW solar PV array requires about 5-7 acres of land, according to the Solar Energy Industries Association (SEIA).
seia.org/initiatives/land-use-solar-development/…
Again, according to the SEIA, solar had a capacity factor of 0.232 last year in the U.S., — by far the poorest performance of any energy source.
What this means is that solar PV arrays only operated at full power 23.2% of the year in 2023 due to variable weather conditions and sky cover.
By using the same calculations as above, a 1,000 MW solar PV array would occupy some 5,000-7,000 acres of land (mean of ~6,000 acres), all the while powering 193,523 homes, some 582,667 fewer homes than if it were nuclear power.
Yikes, that doesn't sound very efficient.
Does, it?
But "what about the wind," they wail?
Let's run the numbers!
A single utility-scale wind turbine occupies ~80 acres of land, which each turbine given a 2.5 MW rating.
A 1,000 MW onshore wind farm would require about 400 2.5-MW turbines occupying some 32,000 acres of land area.
And, according to the EIA, wind had a capacity factor of 0.332 in 2023, meaning that U.S. utility-scale wind farms operated at full power capacity for 33.2% of the year last year.
If we employ the same methods as before, we'll find that a 1,000 MW wind farm could power about 277,143 homes for one year.
Therefore, a 1,000 MW wind farm would power 499,047 fewer homes than a 1,000 MW nuclear facility while occupying over 50 times as much land area.
That's not exactly efficient either, now, is it?
No wonder lefties want you to think that "math is racist".
Let's run the numbers!
A single utility-scale wind turbine occupies ~80 acres of land, which each turbine given a 2.5 MW rating.
A 1,000 MW onshore wind farm would require about 400 2.5-MW turbines occupying some 32,000 acres of land area.
And, according to the EIA, wind had a capacity factor of 0.332 in 2023, meaning that U.S. utility-scale wind farms operated at full power capacity for 33.2% of the year last year.
If we employ the same methods as before, we'll find that a 1,000 MW wind farm could power about 277,143 homes for one year.
Therefore, a 1,000 MW wind farm would power 499,047 fewer homes than a 1,000 MW nuclear facility while occupying over 50 times as much land area.
That's not exactly efficient either, now, is it?
No wonder lefties want you to think that "math is racist".

Into the Night
Verified User
It is not possible to measure the temperature of the Earth, or of a State. There is no 'should be'.The "climate emergency" during Christmas Eve of 1955 was particularly bad.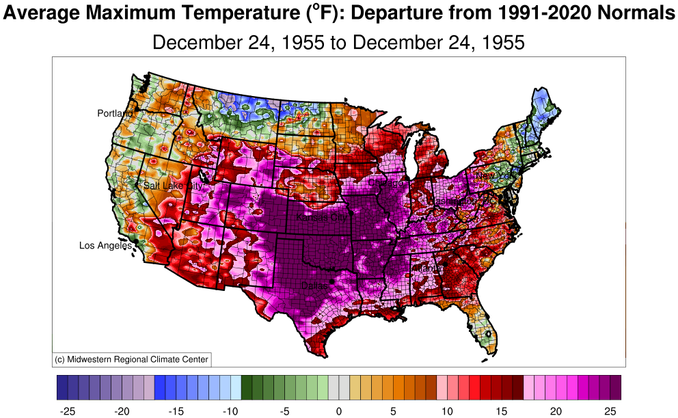

It was ≥70° in 23 states.
It was 93° in TX; 91° in OK; 90° in KS; 85° in AZ, CO, FL and LA; 84° in AR, CA and NM; 83° in NV; 81° in MS; 80° in AL and GA; 79° in MO; 77° in TN; 76° in SC;
73° in KY and NC; 71° in VA; and 70° in IL, OH and WV.
The highs of 90° in Ashland, Kansas and 91° in Gage, Oakwood and Taloga, Oklahoma set monthly record highs for those states which still stand.
Temperatures were running 20-30°+ above average below the 40th parallel.

Argument from randU fallacy.
It is not possible to measure the temperature of the Earth, or of a State. There is no 'should be'.
Is that so?
Into the Night
Verified User
Climate cannot change. It is not possible to measure the temperature of the Earth. Argument from randU fallacy.Currently, climate is apparently changing at 1/20,000th of a degree per day.
Can anybody please explain why this is an 'emergency'?
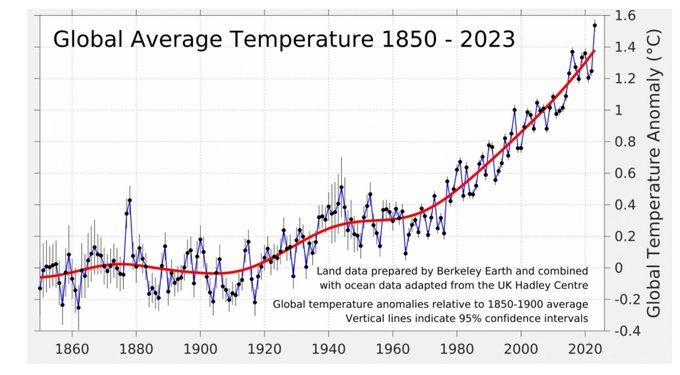
Climate cannot change. It is not possible to measure the temperature of the Earth.
Is that right?
Into the Night
Verified User
It is not possible to measure the temperature of the Northeast States.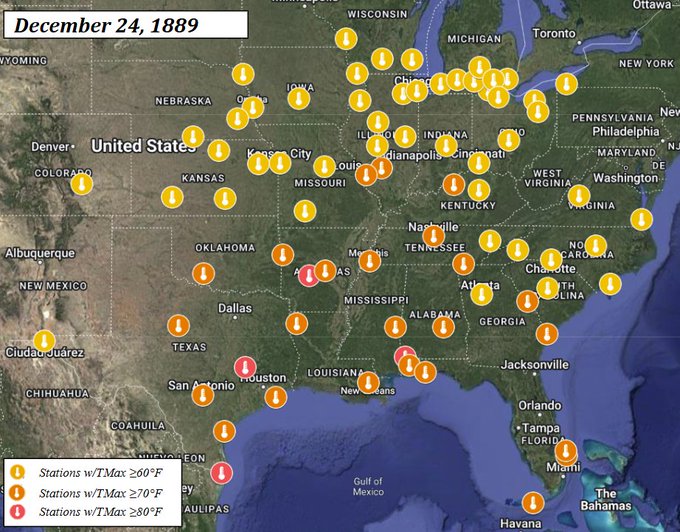
Christmas Eve in 1889 was the mildest on record for much of the Great Lakes and the Corn Belt.
Temperatures topped 60° in every state east of the Rockies, except for the Dakotas, Minnesota and Northeast.
Daily record high maximums were set from Texas to Michigan.
By state, these included:
• Hot Springs, AR: 82°
• Concordia, KS: 68°
• Louisville, KY: 71°
• Lexington, KY: 68°
• Aurora, IL: 70°
• Chicago, IL: 64°
• Moline, IL: 65°
• Peoria, IL: 65°
• Springfield, IL: 67°
• Indianapolis, IN: 68°
• Davenport, IA: 65°
• Des Moines, IA: 69°
• Dubuque, IA: 67°
• Sioux City, IA: 62°
• Ann Arbor, MI: 61°
• Benton Harbor, MI: 65°
• Detroit, MI: 61°
• Kalamazoo, MI: 63°
• St. Louis, MO: 73°
• Omaha, NE: 68°
• Columbus, OH: 66°
• Toledo, OH: 65°
• College Station, TX: 83°
• La Crosse, WI: 61°
• Madison, WI: 60°
• Milwaukee, WI: 60°
The following day would be one of the warmest in the northeast on record.
Boston reached 65°.


Into the Night
Verified User
Climate doesn't need 'help'. Climate cannot change.Democrats could help the climate greatly by sacrificing themselves and lowering our carbon footprint. Somehow they just won't do their duty.
Into the Night
Verified User
Zero. The planet does not need 'saving'. It's quite big enough to take care of itself.How many personal sacrifices of your own money, lifestyle and available options are you prepared to make because somebody tells you that doing so will 'save the planet'?
Discuss.
It is not possible to measure the temperature of the Northeast States.
Is that a fact?
Daylight63
Verified User
The "climate emergency" during Christmas Eve of 1955 was particularly bad.

It was ≥70° in 23 states.
It was 93° in TX; 91° in OK; 90° in KS; 85° in AZ, CO, FL and LA; 84° in AR, CA and NM; 83° in NV; 81° in MS; 80° in AL and GA; 79° in MO; 77° in TN; 76° in SC;
73° in KY and NC; 71° in VA; and 70° in IL, OH and WV.
The highs of 90° in Ashland, Kansas and 91° in Gage, Oakwood and Taloga, Oklahoma set monthly record highs for those states which still stand.
Temperatures were running 20-30°+ above average below the 40th parallel.

It's always fun to see the numerically illiterate try to have "insight" on science. It's so sweetly naive.
Climate cannot change.
Can't it?
It's always fun to see the numerically illiterate try to have "insight" on science. It's so sweetly naive.
Is it? Perhaps you should inform any "numerically illiterates" you encounter of any errors you think they've committed.